கணிதம்

பெருக்கல் (நெடுக்காக மற்றும் குறுக்காக - Vertically and Crosswise)

நாம் காலங்காலமாக பள்ளிகளிலும், கல்லூரிகளிலும் கீழ்கண்ட பெருக்கல் முறையைதான் பயன்படுத்தி வருகிறோம்.

வழக்கமான முறை

           411  x 201
----------------------
          411
        000
      822
----------------------
      82611
----------------------
இதையே "நெடுக்காக மற்றும் குறுக்காக" சூத்திரம் மூலமாக மிக எளிதாக, வேகமாக கணக்கிட முடியும்.
 

உதாரணம் 1:  61 x 31 இரண்டு எண்களை பெருக்குவதாக கொள்வோம்.

            6 1
            3 1 x
------------------------------------
(3x6) : (3x1)+(1x6) : (1x1)

18 : 9 : 1

=1891
 

வழிமுறை:

படி 1 : மேலிருந்து கீழாக நெடுக்காக உள்ள வலபக்க இலக்கங்களை பெருக்கவும், அதாவது (1x1)=1.
படி 2 : மேலேயுள்ள இரு இலக்கங்களை அதன் குறுக்குவாட்டில் உள்ள இலக்கங்களோடு பெருக்கி அதன் கூடுதலை கானவும்,அதாவது (3x1) + (1x6) = 9
படி 3 : நெடுக்காக உள்ள இடப்பக்க இலக்கங்களை பெருக்கவும், அதாவது (3x6) =18 எனவே, 61 x 31 = 1891

---

உதாரணம் 2: 13 x 14 இரண்டு எண்களை பெருக்குவதாக கொள்வோம்.

            1 3
            1 4 x
------------------------------------
(1x1) : (1x3)+(4x1) : (4x3)

1 : 7 : 12

=182

வழிமுறை:

படி 1 : முதலில்நெடுக்காக உள்ள வலபக்க இலக்கங்களை பெருக்கவும். (4x3)=12. இதில் , 2 ஐ விட்டுவிட்டு மீதி 1 ஐ அடுத்த எண்ணிற்கு carry over செய்ய வேண்டும்.
படி 2 : குறுக்குவாட்டில் உள்ள இலக்கங்களை பெருக்கி கூட்டவும்.அத்துடன் carry over செய்த 1 ஐ கூட்டவும். (1x3)+(4x1) = 3 + 4 = 7
படி 3 : நெடுக்காக உள்ள இடப்பக்க இலக்கங்களை பெருக்கவும். (1x1)=1 எனவே,   13 x 14 = 182
இதே முறையை பயன்படுத்தி மூன்று மற்றும் அதற்கு மேற்பட்ட இலக்கங்களை கொண்ட எண்களுக்கான பெருக்கல் பலனை சுலபமாக காணலாம்.

---

உதாரணம் 3:411 x 301 இரண்டு எண்களை பெருக்குவதாக கொள்வோம்.

            4 1 1
            2 0 1 x
---------------------------------------------------------------------------------
(2x4) : (0x4) + (2x1) : (1x4) + (0x1)+ (2x1) : (1x1)+(0x1) : (1x1)

8 : 2 :  6 : 1 : 1

=82611

வழிமுறை:

படி 1 : நெடுக்காக உள்ள வலபக்க இலக்கங்களை பெருக்கவும் (1x1) =1.
படி 2 : குறுக்குவாட்டில் உள்ள இலக்கங்களை பெருக்கி கூட்டவும் 1x1)+(0x1) =1
படி 3 : குறுக்கு மற்றும் நெடுக்காக உள்ள இலக்கங்களை பெருக்கி கூட்டவும்
(1x4) + (0x1)+ (2x1)  = 6 படி 4 : குறுக்குவாட்டில் உள்ள இலக்கங்களை பெருக்கி கூட்டவும் (2x1) : (1x4)  = 2
.
படி 5 : நெடுக்காக உள்ள இடப்பக்க இலக்கங்களை பெருக்கவும் (2x4) = 8
எனவே, 411 x 201 = 82611

---

உதாரணம் 4: 301 x 232 இரண்டு எண்களை பெருக்குவதாக கொள்வோம்.

           301
           232 x
---------------------------------------------------------------------------------
(2x3) : (3x3) +(2x0) : (2x3) +(3x0) +(2x1) : (2x0)+(3x1) : (2x1)

6 : 9 : 8 : 3 : 2

=69832

வழிமுறை:

படி 1 : நெடுக்காக உள்ள வலபக்க இலக்கங்களை பெருக்கவும். (1x2) = 2.
படி 2 : குறுக்குவாட்டில் உள்ள இலக்கங்களை பெருக்கி கூட்டவும்.(2x0)+(3x1) = 3
படி 3 : குறுக்கு மற்றும் நெடுக்காக உள்ள இலக்கங்களை பெருக்கி கூட்டவும்.(2x3) +(3x0) +(2x1) = 8
படி 4 : குறுக்குவாட்டில் உள்ள இலக்கங்களை பெருக்கி கூட்டவும். (3x3) +(2x0) = 9
படி 5 : நெடுக்காக உள்ள இடப்பக்க இலக்கங்களை பெருக்கவும். (2x3) = 6
எனவே,301 x 232 = 69832

---

உதாரணம் 5: 0.0812 x 0.032 இரண்டு எண்களை பெருக்குவதாக கொள்வோம்.

           00812
           00032 x
---------------------------------------------------------------------------------
(8x0) : (8x3) +(1x0) : (8x2) +(1x3) +(2x0) : (1x2)+(2x3) : (2x2)

0 : 24 : 19 : 8 : 4

=0.0025984

வழிமுறை:

படி 1 : நெடுக்காக உள்ள வலபக்க இலக்கங்களை பெருக்கவும். (2x2)=2
படி 2 :குறுக்குவாட்டில் உள்ள இலக்கங்களை பெருக்கி கூட்டவும்.(1x2)+(2x3)=8
படி 3 : குறுக்கு மற்றும் நெடுக்காக உள்ள இலக்கங்களை பெருக்கி கூட்டவும்.(8x2) +(1x3) +(2x0) =19. இதில் , 9 ஐ விட்டுவிட்டு மீதி 1 ஐ அடுத்த எண்ணிற்கு carry over செய்ய வேண்டும்.
படி 4 : குறுக்குவாட்டில் உள்ள இலக்கங்களை பெருக்கி கூட்டவும்.அத்துடன் carry over செய்த 1 ஐ கூட்டவும். (8x3) +(1x0)=24 + (1)= 25. இதில் , 5 ஐ விட்டுவிட்டு மீதி 2 ஐ அடுத்த எண்ணிற்கு carry over செய்ய வேண்டும்..
படி 5 : நெடுக்காக உள்ள இடப்பக்க இலக்கங்களை பெருக்கவும். அத்துடன் carry over செய்த 1 ஐ கூட்டவும். (8x0)=0 + (2) = 2
எனவே ஏழு தசமத்தை தாண்டி புள்ளி வைக்கவும், 0.0812 x 0.032 = 0.0025984

---

உதாரணம் 6:302 x 811 இரண்டு எண்களை பெருக்குவதாக கொள்வோம்.

இங்கு,302 என்ற மூன்றிலக்க எண்ணை 3 ஐ ஒரு இலக்கமாகவும், 02 ஐ ஒரு இலக்கமாகவும் கொண்டு 3(02) என இரண்டிலக்க எண்ணாக மாற்றிகொள்வோம்.
அதே போல், 811 என்ற மூன்றிலக்க எண்ணை 8 ஐ ஒரு இலக்கமாகவும், 11 ஐ ஒரு இலக்கமாகவும் கொண்டு 8(11) என இரண்டிலக்க எண்ணாக மாற்றிகொள்வோம்.

           3(02)
           8(11) x
----------------------------------------
(8x3) : (11x3)+(8x02) : (11x02)

24 : 49 : 22

=244922

வழிமுறை:

படி 1 : நெடுக்காக உள்ள வலபக்க இலக்கங்களை பெருக்கவும். (11x02)=22
படி 2 :குறுக்குவாட்டில் உள்ள இலக்கங்களை பெருக்கி கூட்டவும்.(11x3)+(8x02)=49
படி 3 : நெடுக்காக உள்ள இடப்பக்க இலக்கங்களை பெருக்கவும். (8x3)=24 எனவே,302 x 811 = 244922.

Algebraic proof :

Two Digit Number

Let the two numbers be (ax+b) and (cx+d). Note that x = 10.
Now consider the product ,
(ax + b) (cx + d) = ac.x² + adx + bcx + b.d
= ac.x² + (ad + bc)x + b.d

Three Digit Number

Let the two numbers be (ax² + bx + c) and (dx² + ex + f). Note that x=10
Now consider the product ,
ax² + bx + c
x dx² + ex + f
‾‾‾‾‾‾‾‾‾‾‾‾‾
ad.x4+bd.x³+cd.x²+ae.x³+be.x²+ce.x+af.x²+bf.x+cf
= ad.x⁴ + (bd + ae). x³ + (cd + be + af).x² + (ce + bf)x + cf

நான்கால் வகுபடும் தன்மை

ஓர் எண் 4 ஆல் வகுபடுமா, இல்லையா என்பதை கீழ்கண்ட, மூன்று வழிகளில் காணமுடியும்.
   அ. சாதாரண முறை
   ஆ. சுலப முறை
   இ. வேத கணித முறை ("கடைசி மற்றும் கடைசிக்கு முன்னர் இருமடங்கு")

அ.சாதாரண முறை:

உதாரணம் 1: எண் 12345678, நான்கால் வகுபடுமா?

12345678 என்ற எண்ணை சாதாரண முறையில் 4 ஆல் வகுத்து மீதி வரவில்லையெனில் அவ்வெண் 4 ஆல் வகுபடும்.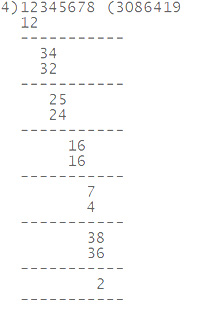

வழிமுறை :

ஈவு 3086419 மீதி 2, எனவே 12345678 ஆனது 4 ஆல் வகுபடாது.

---

ஆ.சுலப முறை

உதாரணம் 1: எண் 12345678, நான்கால் வகுபடுமா?

எண்ணின் கடைசி இரண்டு இலக்கமானது 4 ஆல் வகுப்பட்டால் அவ்வெண்ணானது 4 ஆல் வகுபடும்
இங்கு, 12345678 ன் கடைசி இரண்டு இலக்கம் 78 ஆகும், 78 ஆனது 4 ஆல் வகுப்படவில்லை, எனவே 12345678 என்ற எண் 4 ஆல் வகுபடாது. 

---

இ.வேதகணித முறை ("கடைசி மற்றும் கடைசிக்கு முன்னர் இருமடங்கு")

"கடைசி மற்றும் கடைசிக்கு முன்னர் இருமடங்கு" என்ற சூத்திரமூலமாக எவ்வளவு பெரிய எண்ணாக இருந்தாலும், அவ்வெண்ணானது 4 ஆல் வகுப்படுமா இல்லையா என்பதை சுலபமாக கண்டறிய முடியும்.

வழிமுறை :

ஓர் எண்ணின் கடைசி இலக்கத்தையும், அதற்கு முன்னர் உள்ள இலக்கதின் இருமடங்கையும் கூட்டி 4 ஆல் வகுத்து மீதி பூஜ்ஜியம் வந்தால், அவ்வெண்ணானது நான்கால் வகுப்படும்.

உதாரணம் 1: எண் 9447968792, நான்கால் வகுபடுமா?

எண் 9447968792 ன் கடைசி இலக்கமானது 2 ஆகும். அத்துடன் கடைசிக்கு முன்னர் உள்ள 9 இன் இருமடங்கான 18 ஐக் கூட்ட, (18+2=20) 20 வருகிறது. இந்த 20 ஆனது 4 ஆல் வகுபடும். எனவே 9447968792 ஆனது 4 ஆல் வகுபடும்.

உதாரணம் 2: எண் 999939283229849781, நான்கால் வகுபடுமா?

எண் 999939283229849781 ன் கடைசி இலக்கமானது 1 ஆகும். அத்துடன் கடைசிக்கு முன்னர் உள்ள 8 ன் இருமடங்கான 16 யும் கூட்ட (16+1=17) 17 வருகிறது. இந்த 17 ஆனது 4 ஆல் வகுபடாது. எனவே 999939283229849781 ஆனது 4 ஆல் வகுபடாது.

கணிதப்புதிர்

Tower of Hanoi 

நண்பர்களே நாமது குழந்தைகள் செய்து மகிழ மிகவும் சுவையான கணிதப்புதிர் விளையாட்டினை பார்ப்போம் இந்த புதிர் இந்தியாவின் காசி நகரை மையமாக வைத்து தோன்றியது

நிலையாக நிறுத்தி வைக்கப்பட்ட மூன்று குச்சிகள் உள்ளது அதில் ஒரு குச்சியில் ஒரு சிறு தட்டு அதன் மேல் சற்று பெரிய தட்டு அதன் மேல் இன்னும் கொஞ்சம் பெரிய தட்டு என வரிசைகிரமமாக ஏறு வரிசையில் அமைந்த சில தட்டுகள் உள்ளது இப்போது புதிர்  என்னவெனில்

மேலிருந்துதான் தட்டுக்களை  வரிசையாகத்தான் எடுக்க வேண்டும். நடுவில் உள்ளதையோ அடியில் உள்ளதையோ மாற்றி மாற்றி  எடுக்க கூடாது.

ஒருமுறை ஒரு தட்டை மட்டும்  எடுத்து மற்றொரு குச்சியில் பொருத்த வேண்டும்.

பெரியதட்டின் மேல்தான் சிறிய தட்டை வைக்க வேண்டும் சிறியதட்டின் மேல் பெரிய தட்டினை வைக்க கூடாது .

அருகில் உள்ள படத்தினை பாருங்கள் அடியில் உள்ள பழுப்பு மிக பெரிய தட்டு நீலம் அதைவிட சிறியவை நீல தட்டும் மஞ்சள் தட்டும் கடைசியில் உள்ள சிவப்புதட்டு எல்லாவற்றையும் விட மிக மிக சிறியது முதலில் சிவப்புத்தட்டினை எடுத்து காலியாக உள்ள இரண்டு குச்சிகளில் ஏதாவது ஒன்றில் பொருத்தவேண்டும் அடுத்தபடியாக மஞ்சள் தட்டினை எடுக்க வேண்டும் மஞ்சள்தட்டினை சிவப்புதட்டின் மீது பொருத்த முடியாது  ஏன் எனில் மஞ்சள் தட்டினைவிட சிவப்புதட்டு சிறியது எனவே மீதி காலியாக உள்ள குச்சியில் பொருத்த வேண்டும் . இப்பொழுது நீல தட்டினை  எடுக்க முடியாது ஏன் எனில் நீலத்தட்டினை எடுத்து எதன் மீதும் பொருத்த முடியாது மஞ்சளும், சிவப்பும் நீலத்தட்டினைவிட சிறியது.  எனவே மிகச்சிறிய சிவப்பு தட்டினை எடுத்து அதைவிட பெரிய தட்டான மஞ்சள் தட்டின் மேல் வைக்க வேண்டும் இப்பொழுது நீல தட்டினை  எடுத்து காலியாக உள்ள குச்சியின் மேல் பொருத்தலாம் மீண்டும் இதே வழிமுறையை தொடர வேண்டும் .

இந்த புதிருக்கான தீர்வு 2ⁿ – 1 கணித சூத்திரம் ஆகும்

மூன்று தட்டுகள் எனில்  7 நகர்தல்களில் அதே வரிசை கிரமத்தில் மற்றொரு இடத்தில் நகர்த்த வேண்டும்

 2³-1=8-1=7

 நான்கு தட்டுகள்  எனில் 15 நகர்தல்களில் செய்ய வேண்டும் மூன்று அல்லது நான்கு தட்டுகள் இருந்தால்   எளிமையாக செய்யலாம் ஆனால் தட்டுகளின்  எண்ணிக்கை அதிகரித்தால்  இதை செய்வது கடினம் முறையான பயிற்சி இருந்தால் மட்டுமே குறிப்பிட்ட நகர்தல்களில் செய்ய முடியும்

வினாக்களுக்கு விடை தரும் இணையம் (கணித பாடம் தொடர்பான)

 

 மாணவர்கள் தங்களது கணித பாடம் தொடர்பாக எழுகின்ற  சந்தேகங்கள் மற்றும் பிரச்சனைகளுக்கு சில நொடிப்பொழுதுகளில் மிக இலகுவாக தீர்த்து வைக்கிறது இந்த இணையம் . மாணவர்களுக்கு இந்த இணையம் மிக பெரிய சேவையினை செய்கின்றது என்றால் அது மிகையாகது 

 

இந்த இணையத்தில் கணித பாடம் தொடர்பான உங்களின் வினாக்களை type செய்து பின்னர் அதன் கீழே பாட அலகினை தெரிவு செய்து பின்னர் answer என்பதை கிளிக் செய்தவுடன் விடை தோன்றும்
 

(கீழே உள்ள படத்தினை காண்க )

உங்களுக்கு மிக தெளிவான விளக்கத்துடன் விடையினை பெறும் வசதியும் உண்டு .  கணித பாடத்தின் முழு பாட அலகினையும் கொண்டுள்ளமை இதன் மற்றுமொரு சிறப்பம்சம் ஆகும் . 

அத்துடன் இந்த தளத்தில் உங்களை பதிவு செய்து உங்களின் வினாக்களையும் அதற்கான பதில்களையும் சேமிக்க முடியும் . ஏற்கனவே தீர்க்கப்பட்ட பிரச்சனைகளையும் பார்க்க முடியும் . 

லிங்க் http://www.mathway.com/

http://www.mathway.com/problem.aspx?p=basicmath

நினைத்த எண்ணினை கண்டுபிடிக்கும் சுவையான விளையாட்டு

நண்பர்களே பள்ளி நாட்களில்  நாம் விளையாடிய மிகவும் சுவையான கணிதவிளையாட்டு நினைத்த எண்ணினை கண்டுபிடிக்கும் விளையாட்டு  இந்த விளையாட்டைவிளையாட பல வகை முறைகள் இருப்பினும்  99  ஐ தவிர அனைத்து எண்களுக்கும்பொருந்தும் எளிய முறையை உங்களிடம் பகிர்ந்து கொள்கிறேன்.

 

விளையாடும் முறை

உங்களின் நண்பர்களையோ உறவினர்களையோ ஏதாவது ( 99 தவிர ) ஒரு எண்ணினைமனதில் நினைத்துக்கொள்ளச்சொல்லுங்கள் பின்பு கீழே கொடுக்கப்பட்ட விதிகளைமனதிலேயே பின்பற்ற சொல்லுங்கள் கடைசியில் கிடைக்கும் விடையை மட்டும்சொல்லச்சொல்லுங்கள் அதிலிருக்கும் பூச்சியங்களை  நீக்கி விட்டால் கிடைக்கும் எண்தான்மனதில்  நினைத்த எண் ஆகும்  

விதிமுறைகள்

1 . மனதில் நினைத்த எண்ணினை இருமடங்கு ஆக்குக

2 . 4 ஐ கூட்டுக

3 . 5 ஆல் பெருக்குக

4 . 12 ஐ கூட்டுக

5 . 10 ஆல் பெருக்குக

6 . 320 ஐ கழிக்க

கிடைக்கும் விடையை சொல்லச்சொல்லுங்கள் அதிலிருக்கும் பூச்சியங்களை நீக்கி விட்டால்மனதில்  நினைத்த எண் கிடைக்கும்

எடுத்துக்காட்டு

மனதில் நினைத்த எண் 63 எனில் அதை இரு மடங்காக்கினால் கிடைப்பது 126 அதனுடன்  4 ஐ கூட்டினால் கிடைப்பது 130 அதை  5 ஆல் பெருக்க கிடைப்பது  650  அதன்னுடன்  12ஐ கூட்ட கிடைப்பது 662 அதை 10 ஆல் பெருக்கினால் கிடைப்பது 6620 அதிலிருந்து 320 ஐகழித்தால் கிடைப்பது  6300  ஆகும் இதில் உள்ள பூச்சியங்களை  நீக்க கிடைப்பது 63 இதுதான் மனதில் நினைத்த எண்.